In order to have a complete theory of gravity, we need to know
The first question is answered by postulating that free particles [ i.e. no
force other than gravity ] follow timelike or null geodesics. We will see later that this is equivalent to Newton's law
in the week field limit [ 
].
The second requires the analogue
of 
. We first consider the vacuum case [ 
]
.
The easiest way to do this is to compare the geodesic deviation equation derived in the last section
with its Newtonian analogue.
In Newtonian theory the acceleration of two
neighboring particles with position vectors 
and 
are:
so the separation evolves according to:
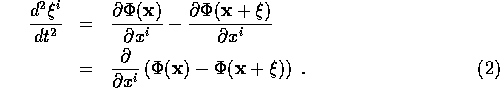
This gives us
since
This clearly is analogous to the geodesic deviation equation
provided we relate the quantities 
and
Both quantities have two free indices, although the Newtonian index runs from 1 to 3 while in the General Relativity case it runs from 0 to 3.
The Newtonian vacuum equation is which implies that
so we can write
Since 
is arbitrary we end up with
These are the vacuum field equations .